Equilateral Triangle
Pronunciation: /ˌi.kwəˈlæ.tər.əl ˈtraɪˌæŋ.gəl/ Explain
|
An equilateral triangle is a triangle where all of the sides are the same length.[3] |
| Property | Equation | Description | ||
|---|---|---|---|---|
| Length of the sides | 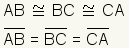 | The length of the sides of an equilateral triangle are equal by definition. The length of a side of an equilateral triangle is conventionally represented by the variable s. | ||
| Angles | 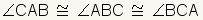 | The angles of an equilateral triangle are congruent. | ||
| Measure of the angles | 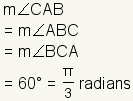 | The angles of an equilateral triangle all measure 60° or  . . | ||
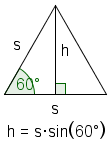
| Altitude | 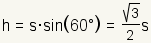 |
| ||
| Area | 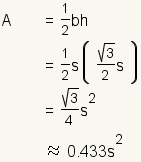 | The area of an equilateral triangle is  . Using the formula for the altitude, . Using the formula for the altitude,  . . | ||
| Inradius | 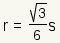 | The inradius of an equilateral triangle is 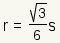 . . | ||
| Circumradius | 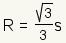 | The circumradius of an equilateral triangle is 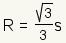 . . | ||
| Area of the incircle | 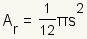 | The area of the incircle of an equilateral triangle is 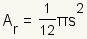 . . | ||
| Area of the circumcircle | 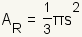 | The area of the circumcircle of an equilateral triangle is 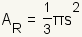 . . | ||
| Table 1 | ||||
Constructing an Equilateral Triangle
| Step | Example | Description | Justification |
| 1 |  |
Start with a line segment | |
| 2 |  |
Label the end points A and B. | |
| 3 | 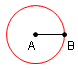 |
Construct a circle with the center at A and the radius the length of segment AB. | Euclid's Elements Book 1 Postulate 3: A circle can be drawn with any center and any radius. |
| 4 | 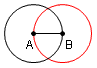 |
Construct a circle with the center at B and the radius the length of segment AB. | Euclid's Elements Book 1 Postulate 3: A circle can be drawn with any center and any radius. |
| 5 | 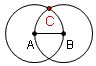 |
Label an intersection of the two circles C. | |
| 6 | 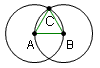 |
Construct a line segment AC and BC. This forms triangle ABC. | Euclid's Elements Book 1 Postulate 1: A straight line can be drawn from any point to any point. |
| 7 | Since they are radii of the same circle, the line segment AC is the same length as the line segment AB. Similarly, the line segment BC is the same length as the line segment AB. | Euclid's Elements Book 1 Definition 15: A circle is all points equidistant from a center point. | |
| 8 | Since AB ≡ AC and AB ≡ BC, then it must be true that AC ≡ BC. | Euclid's Elements Book 1 Common Notion 1: If A = B and B = C then A = C. | |
| 9 | By the definition of an equilateral triangle, the triangle ABC is equilateral. | Euclid's Elements Book 1 Definition 20: An equilateral triangle is a triangle where the length of all three sides is the same. | |
| Q.E.D. | |||
| Table 2 | |||
References
- McAdams, David E.. All Math Words Dictionary, equilateral triangle. 2nd Classroom edition 20150108-4799968. pg 71. Life is a Story Problem LLC. January 8, 2015. Buy the book
- equilateral triangle. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 7/9/2018. http://www.merriam-webster.com/dictionary/equilateral triangle. Buy the book
- Casey, John, LL.D., F.R.S.. The First Six Books of the Elements of Euclid. pp 8,11-12. Translated by Casey, John, LL.D. F.R.S.. www.archive.org. Hodges, Figgis & Co.. 1890. Last Accessed 7/9/2018. http://www.archive.org/stream/firstsixbooksofe00caseuoft#page/8/mode/1up/search/equilateral. Buy the book
- Le Clerc, Sébastien; Nattes, John Claude; Pyne, W. H.. Nattes's practical geometry, or, Introduction to perspective. pg 11. www.archive.org. W. Miller. 1805. Last Accessed 7/9/2018. http://www.archive.org/stream/nattesspractical00leclrich#page/11/mode/1up/search/equilateral. Buy the book
More Information
- Euclid. Elements Book 1, Proposition 1: To construct an equilateral triangle on a given finite straight line.. mathcs.clarku.edu. 3/12/2009. https://mathcs.clarku.edu/~djoyce/elements/bookI/propI1.html.
- Euclid of Alexandria. Elements. mathcs.clarku.edu. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.
Cite this article as:
McAdams, David E. Equilateral Triangle. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/e/equilateraltriangle.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/20/2019: Updated expressions and equations to match new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
1/26/2010: Added "References". (McAdams, David E.)
12/18/2008: Added 'Properties of an Equilateral Triangle' and changed figure to manipulative. (McAdams, David E.)
8/20/2007: Added construction of an equilateral triangle. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License