Hyperbola
Pronunciation: /haɪˈpɜr.bə.lə/ Explain
|
A hyperbola is a conic section formed by intersecting a right circular conic surface and a plane that intersects both halves of the cone. The equations most often used for a hyperbola are:   |
Graph of a Hyperbola
|
A hyperbola can be defined as a set of points where the ratio of the distance from a fixed line called the directrix and the distance from the point is equal to the ratio of c to a. The equation for the directrices of a hyperbola with an east/west opening is 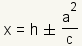 . .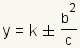 . .The foci for a hyperbola are the points at
In manipulative 1, click on the check box marked 'Show directrices'. Click on the blue point on the hyperbola and drag it. Notice that the ratio remains constant for a particular hyperbola. |
Eccentricity of Hyperbolas
The eccentricity of a hyperbola can be considered as how far the hyperbola deviates from a circle. The larger the eccentricity, the flatter the hyperbolic curve. The formula for the eccentricity of a hyperbolic curve is

Hyperbolas in Nature
| A flashlight makes a cone of light. If a flashlight is held close to a wall and parallel to the wall, the plane of the wall 'cuts' the cone at in such a way that the 'edges' of the light form a hyperbola. | ||
| ||
|
The path of an object in space relative to a much larger object can be a hyperbola. The path of the object is a hyperbolic trajectory if the speed of the smaller object relative to the larger object is more than escape velocity. In actuality, very few hyperbolic trajectories are observed in nature. This is because an object on a hyperbolic trajectory 'breaks free' of the gravitational field of the larger object (in this case the sun). Because it breaks free, the object does not return close to the larger object so is rarely observed. |
Hyperboloid
|
A hyperboloid is a 3-dimensional figure created by rotating a hyperbola about a line. Figures 4 and 5 show two types of hyperboloids. |
|
References
- McAdams, David E.. All Math Words Dictionary, hyperbola. 2nd Classroom edition 20150108-4799968. pg 92. Life is a Story Problem LLC. January 8, 2015. Buy the book
More Information
- McAdams, David E.. Conic Section. allmathwords.org. Life is a Story Problem LLC. 3/12/2009.
Cite this article as:
McAdams, David E. Hyperbola. 4/22/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/h/hyperbola.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
- Hyperbolic Conic Section. Unknown.
- Hyperboloid of One Sheet: Svdmolen, https://en.wikipedia.org. Licensed under the terms of the GNU Free Documentation License, Version 1.2 or any later version. https://en.wikipedia.org/wiki/File:HyperboloidOfOneSheet.png.
- Hyperboloid of Two Sheets: Svdmolen, https://en.wikipedia.org. Licensed under the terms of the GNU Free Documentation License, Version 1.2 or any later version.
- Flashlight Making a Hyperbola: Dave Clauson. Used with permission. Do not copy.
Revision History
4/22/2019: Update equations and expressions to new format. (McAdams, David E.)3/17/2019: Fixed broken link. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/16/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/8/2010: Added "References". (McAdams, David E.)
1/7/2010: Added "References". (McAdams, David E.)
12/12/2008: Added hyperboloid. (McAdams, David E.)
12/10/2008: Corrected equations. Added hyperbolas in nature (McAdams, David E.)
11/26/2008: Change equations to images. (McAdams, David E.)
8/8/2008: Added paragraph on eccentricity. Added https://www.allmathwords.org/conicsection.html to More Information. Added manipulative 1. Converted equation to hot_eqn (McAdams, David E.)
7/1/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License

 for a hyperbola with an east/west
opening and
for a hyperbola with an east/west
opening and  for a hyperbola
with a north/south opening.
for a hyperbola
with a north/south opening.