Reflection

Pronunciation: /rɪˈflɛk.ʃən/ Explain

Click on the blue points and drag them to change the figure.

What happens if the line of reflection intersects the objects being reflected?
Manipulative 1 - Reflection Across a Line Created with GeoGebra.

A reflection is a geometric transformation. In a reflection, a geometric object is 'flipped' across a line. The line across which an object is reflected is called the line of reflection or the axis of reflection.

Manipulative 1 shows the reflection of an irregular pentagon across a line. Note that the reflected figure is a mirror image of the original figure.

Properties of Reflections

  • An object and its reflection are symmetrical about the line of reflection.
  • An object and its reflection are congruent.
  • An object and its reflection are
    • similar.
  • If a reflected object is reflected again about the same line of reflection, the resulting object is coincidental with the original object.

How to Construct a Reflection

Constructing the Reflection of a Point
StepFigureDescription
1A line of reflection and a point A not on the line of reflection. We will be constructing the reflection of point A across the line of reflection.
2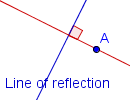A line of reflection and a point A not on the line of reflection. A line perpendicular to the line of reflection passing through point A has been drawn. Construct a line perpendicular to the line of reflection that passes through point A.
3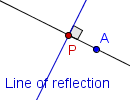A line of reflection and a point A not on the line of reflection. A line perpendicular to the line of reflection passing through point A has been drawn. The intersection of the two lines is marked as point P. Mark the intersection of the perpendicular lines as P.
4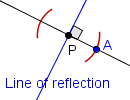A line of reflection and a point A not on the line of reflection. A line perpendicular to the line of reflection passing through point A has been drawn. The intersection of the two lines is marked as point P. Two arcs on the circle with center at point P and radius of PA have been drawn that intersect the perpendicular line. Use a compass with the point on P and the stylus on point A. Without removing the point from P, draw a circular arc on the opposite side of the perpendicular line.
5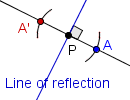A line of reflection and a point A not on the line of reflection. A line perpendicular to the line of reflection passing through point A has been drawn. The intersection of the two lines is marked as point P. Two arcs on the circle with center at point P and radius of PA have been drawn that intersect the perpendicular line. The intersection of the arc opposite point A and the perpendicular line is marked A'. Mark the intersection of the arc and the perpendicular line as A'.
Table 1: Constructing the reflection of a point.

How to Construct the Reflection of a Triangle
StepFigureDescription
1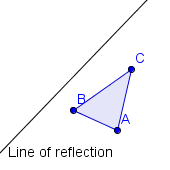A line of reflection and a triangle ABC. We will be constructing the reflection of triangle ΔABC across the line of reflection.
2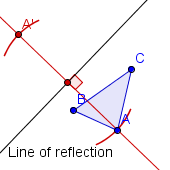A line of reflection and a triangle ABC. Point A' is the reflection of A across the line of reflection. Construct the reflection of A across the line of reflection (see table 1). Label the reflected point A'.
3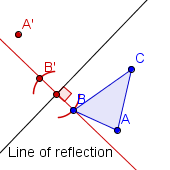A line of reflection and a triangle ABC. Point B' is the reflection of B across the line of reflection. Construct the reflection of B across the line of reflection. Label the reflected point B'.
4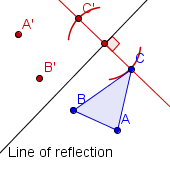A line of reflection and a triangle ABC. Point C' is the reflection of C across the line of reflection. Construct the reflection of C across the line of reflection. Label the reflected point C'.
5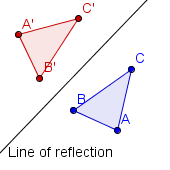A line of reflection and a triangle ABC. Points A', B' and C' are connected with line segments forming triangle A'B'C'. Use a straight edge to connect points A', B' and C' with line segments. The triangle ΔA'B'C' is the reflection of triangle ΔABC across the line of reflection.
Table 1: Constructing the reflection of a triangle.

References

  1. McAdams, David E.. All Math Words Dictionary, reflection. 2nd Classroom edition 20150108-4799968. pg 153. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

Cite this article as:

 McAdams, David E. Reflection. 5/2/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/r/reflection.html.

Image Credits

Revision History

5/2/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/4/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra app. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
1/13/2009: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License