TriÃĄngulo equilÃĄtero
|
Un triÃĄngulo equilÃĄtero es un triÃĄngulo donde estÃĄn la misma longitud todos los lados. Chasque encendido los puntos azules en el manipulante1 y arrÃĄstrelos para cambiar la figura. |
| CaracterÃstica | EcuaciÃģn | DescripciÃģn | ||
|---|---|---|---|---|
| Longitud de los lados | 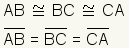 |
La longitud de los lados de un triÃĄngulo equilÃĄtero es igual por definiciÃģn. La longitud de un lado de un triÃĄngulo equilÃĄtero es representada convencionalmente por el variable s. | ||
| Ã?ngulos | 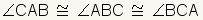 | Los ÃĄngulos de un triÃĄngulo equilÃĄtero son congruentes. | ||
| Medida de los ÃĄngulos | 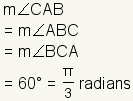 | Los ÃĄngulos de un triÃĄngulo equilÃĄtero toda la medida 60° o  . . | ||
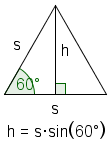
| Altitud | 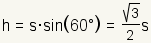 |
| ||
| Ã?rea | 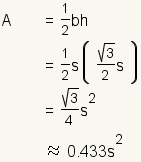 | El ÃĄrea de un triÃĄngulo es  . Usando la fÃģrmula para la altitud . Usando la fÃģrmula para la altitud  . . | ||
| Radio de circunferencia inscrita | 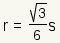 | El radio de circunferencia inscrita de un triÃĄngulo equilÃĄtero es 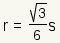 . . | ||
| Radio de circunferencia circunscrita | 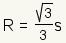 | El radio de circunferencia circunscrita de un triÃĄngulo equilÃĄtero es 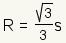 . . | ||
| Ã?rea del circunferencia inscrita | 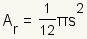 | El ÃĄrea del circunferencia inscrita de un triÃĄngulo equilÃĄtero es 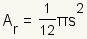 . . | ||
| Ã?rea del circunferencia circunscrita | 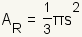 | El ÃĄrea del circunferencia circunscrita de un triÃĄngulo equilÃĄtero es 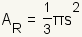 . . | ||
| Cuadro 1 | ||||
Construir un triÃĄngulo equilÃĄtero
| Paso | Ejemplo | DescripciÃģn | JustificaciÃģn |
| 1 |  |
Comience con una recta segmento | |
| 2 |  |
Etiquete los puntos A y B del extremo. | |
| 3 | 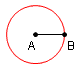 |
Construya un circunferencia con el centro en A y el radio la longitud del segmento AB. | Postulado 3 del libro 1 de los elementos de Euclid: Un circunferencia se puede dibujar con cualquier centro y cualquier radio. |
| 4 | 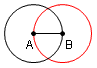 |
Construya un circunferencia con el centro en B y el radio la longitud del segmento AB. | Postulado 3 del libro 1 de los elementos de Euclid: Un circunferencia se puede dibujar con cualquier centro y cualquier radio. |
| 5 | 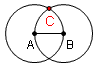 |
Etiquete una intersecciÃģn de los dos circunferencias C. | |
| 6 | 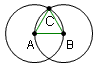 |
Construya una recta AB del segmento y BC. Esto crea el triÃĄngulo del ΔABC. | Postulado 1 del libro 1 de los elementos de Euclid: Una recta recta se puede extraer de cualquier punto a cualquier punto. |
| 7 | Puesto que son radios del mismo circunferencia, la segmento recta AC es la misma longitud que la recta segmento AB. Semejantemente, la recta segmento es BC misma longitud que la recta segmento AB. | Los elementos de Euclid reservan 1 definiciÃģn 15: Un circunferencia es todos los puntos equidistantes de un punto central. | |
| 8 | Desde AB ≡ AC y AB ≡ BC, entonces debe ser verdad que AC ≡ BC. | Los elementos de Euclid reservan 1 nociÃģn comÚn 1: Si A = B y B = C entonces A = C. | |
| 9 | Por la definiciÃģn de un triÃĄngulo equilÃĄtero, el triÃĄngulo ΔABC es equilÃĄtero. | Los elementos de Euclid reservan 1 definiciÃģn 20: Un triÃĄngulo equilÃĄtero es un triÃĄngulo donde estÃĄ igual la longitud de los tres lados. | |
| Q.E.D. | |||
| Cuadro 2 | |||
MÃĄs informaciÃģn
- Euclid. Libro 1, asunto 1 de los elementos: Para construir un triÃĄngulo equilÃĄtero en una recta recta finita dada.. 2009-04-03. D. Joyce, Babelfish.Yahoo.com. http://babbage.clarku.edu/~djoyce/java/elements/bookI/propI1.html.
Citar este artÃculo como:
TriÃĄngulo equilÃĄtero. 2009-04-03. Enciclopedia de Todas las Palabras de la MatemÃĄticas. Life is a Story Problem.org. https://www.allmathwords.org/es/e/equilateraltriangle.html.
Traducciones
crÃĐditos de imagen
- Todas las imÃĄgenes y manipulatives estÃĄn por David McAdams a menos que estÃĐn indicadas de otra manera. Todas las imÃĄgenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisiÃģn
2009-04-03: Traducido automÃĄticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-18: '' CaracterÃsticas agregadas de un triÃĄngulo equilateral '' y de la figura cambiada a manipulante (McAdams, David.)
2007-08-20: ConstrucciÃģn agregada de un triÃĄngulo equilateral (McAdams, David.)
2007-07-12: VersiÃģn inicial (McAdams, David.)
- NavegaciÃģn
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la MatemÃĄticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ÂĐ2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License