Hipérbola: Una sección cónica formó intersecando un plano con ambas mitades de una cónica derecha.

Hipérbola

Cónico con la sección hiperbólica.
Cuadro 1: Sección cónica

Una hipérbola es una sección cónica formada intersecando una superficie cónica circular correcta y un plano que interseque ambas mitades del cono. Las ecuaciones más de uso frecuente para una hipérbola son:

((x-h) ^2)/a- ((y-k) ^2)/b=1
donde está el eje a semi-principal paralelo al eje x, b es el eje semi-de menor importancia paralelo al eje y, y el punto (h, k) es el centro de la hipérbola, y
((y-k) ^2)/b- ((x-h) ^2)/a=1
donde está el eje a semi-de menor importancia paralelo al eje x, b es el eje semi-principal paralelo al eje y, y el punto (h, k) es el centro de la hipérbola.

Gráfico de una hipérbola

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
1 manipulante: Hipérbola. Creado con GeoGebra.

Una hipérbola se puede definir como conjunto de puntos donde está igual el razón de la distancia de una recta fija llamada la directriz y de la distancia del punto al razón de c a a. La ecuación para las directrices de una hipérbola con un este/el del oeste es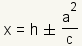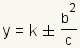

x=h+-a^2/c.
La ecuación para las directrices de una hipérbola con un del norte/al sur la apertura es
y=k+-b^2/c.

Los focos para una hipérbola son los puntos en (h+-c, k) para una hipérbola con un del este/al oeste la apertura y (h, k+-c) para una hipérbola con un del norte/al sur la apertura.

En el manipulante 1, chasque encendido la caja de cheque las “directrices marcadas de la demostración�. Chasque encendido el punto azul en la hipérbola y arrástrelo. Note que el razón sigue siendo constante para una hipérbola particular.

Excentricidad de hipérbolas

La excentricidad de una hipérbola puede ser considerada como hasta dónde la hipérbola se desvía de un circunferencia. Cuanto más grande es la excentricidad, el aplanador la curva hiperbólica. La fórmula para la excentricidad de una curva hiperbólica es

raíz del epsilon=square (1+b^2/a^2)

Hipérbolas en naturaleza

Una linterna que brilla en una pared el borde de la luz forma tan una hipérbola.
Cuadro 2: Hipérbola de la linterna. Cortesía de imagen Dave Clauson, High School secundaria de Cañada del La. Chasque encendido la imagen para una versión más grande.
Una linterna hace un cono de luz. Si una linterna se sostiene cerca de una pared y de un paralelo a la pared, el plano de la pared “corta� el cono en de una manera tal que “afile� de la forma ligera una hipérbola.

Dibujo de un tubo colocado en líquido. El líquido se elabora en el tubo y forma una porción de una curva hiperbólica.
Cuadro 3: Acción de Capilary.
Un líquido en un pequeño tubo es elaborado el tubo por una acción conocida como acción capilary. El líquido forma una curva hiperbólica. Para más información vea la acción capilary en la enciclopedia del Internet de la ciencia.

La trayectoria de un objeto en espacio concerniente a un objeto mucho más grande puede ser una hipérbola. La trayectoria del objeto es una trayectoria hiperbólica si la velocidad del objeto más pequeño concerniente al objeto más grande es más que velocidad de escape. En actualidad, muy poca trayectoria hiperbólica se observa en naturaleza. Esto es porque un objeto en una trayectoria hiperbólica “se rompe libremente� del campo gravitacional del objeto más grande. Porque se rompe libremente, el objeto no vuelve cerca del objeto más grande así que se observa raramente.

Hiperboloide

Hiperboloide de una hoja.
Cuadro 4: Hiperboloide de una hoja. Imagen autorizada debajo de licencia de la documentación del GNU libremente. Chasque encendido la imagen para una versión más grande.

Un hiperboloide es una figura de 3 dimensiones creada girando una hipérbola sobre una recta. Los cuadros 4 y 5 demuestran dos tipos de hiperboloides.

Hiperboloide de dos hojas.
Cuadro 5: Hiperboloide de dos hojas. Imagen autorizada debajo de licencia de la documentación del GNU libremente. Chasque encendido la imagen para una versión más grande.

Más información

  • McAdams, David. Sección cónica. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Conic%20Section.
  • hipérbola. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=hipérbola.
  • Darling, David. hipérbola. The Internet Encyclopedia of Science. 2009-04-03. Traducido automáticamente por babelfish.yahoo.com. http://www.daviddarling.info/encyclopedia/H/hyperbola.html.
  • Clauson, Dave. Secciones cónicas. 2009-04-03. Traducido automáticamente por babelfish.yahoo.com. http://www.clausentech.com/lchs/dclausen/algebra2/conic_sections.htm.

Citar este artículo como:
Hipérbola. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/h/hyperbola.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-12: Hyperboloid agregado (McAdams, David.)
2008-12-10: Ecuaciones corregidas. Hipérbolas agregadas en naturaleza (McAdams, David.)
2008-11-26: Cambie las ecuaciones a las imágenes (McAdams, David.)
2008-08-08: Apartado relativo agregado a excentricidad. https://www.allmathwords.org/conicsection.html agregado a más información. 1. ecuaciones convertidas manipulante agregada al hot_eqn (McAdams, David.)
2008-07-01: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License