Cuartila

El conjunto de datos {1, 3, 4, 4, 5, 7, 9} donde está la primera cuartila 3, los segundos 4 es el la segunda cuartila o mediano, y 7 es la tercera cuartila.
Cuadro 1: Cuartilas

El conjunto de datos {1, 3, 4, 4, 5, 7, 9, 10, 10} donde está la primera cuartila (3+4)/2=3.5, la segunda cuartila o punto medio es los 5, y la tercera cuartila es (9+10)/2=9.5.
Cuadro 2: Cuartilas

Una cuartila es uno de tres valores que divide un grupo de datos en cuatro grupos. Cada grupo tiene el mismo número de elementos. La primera cuartila, también llamada Q1, es un número entre el cuarto más bajo del grupo de datos y el 2do cuarto. LaLa segunda cuartila, también llamada Q2, es un número entre el 2do cuarto del grupo de datos y el 3ro cuarto. La segunda cuartila (Q2) es igual que el punto medio del grupo de datos. La tercera cuartila, también llamada Q3, es un número entre el 3ro cuarto y el 4to cuarto.

Cuartilas y porcentajes

CuartilaPorcentaje
Q125to
Q2 o punto medio50.o
Q375.o
Cuadro 1: Cuartila y porcentaje.

La primera cuartila, Q1, es igual que el 25to porcentaje. La segunda cuartila, Q2, es igual que el 50.o porcentaje. La tercera cuartila, Q3 es igual que el 75.o porcentaje.

Cuartilas calculadoras

Para encontrar las cuartilas de un grupo de datos, el primeros encuentran el punto medio del grupo de datos. Si el grupo de datos tiene un número impar de elementos, utilice el número medio. Si el grupo de datos tiene un número par de elementos, utilice el medio aritmético de los dos números medios. Esto parte el grupo de datos en dos porciones iguales. Ninguna de las dos partes contiene el punto medio. El punto medio es igual que Q2.

Después tome cada mitad del grupo de datos y encuentre el punto medio de esa mitad. El punto medio de la primera mitad del grupo de datos es Q1. El punto medio de la segunda mitad del grupo de datos es Q3.

Ejemplos

PasoFiguraDescripción
1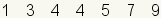1 3 4 4 5 7 9Éste es el grupo de datos a dividir en cuartilas.
21 3 4 4 5 7 9 con los segundos 4 identificados como el centro.Puesto que el grupo de datos tiene un número impar de elementos, escoja el elemento medio para el punto medio (Q2).
31 3 4 4 5 7 9 con 1 3 4 identificados como la primera mitad, 4 identificados como Q2, y 5 7 9 identificados como la segunda mitad.El número medio divide el grupo de datos en dos mitades. Puesto que el número medio es el punto medio, no se incluye por la mitad cualquier.
41 3 4 4 5 7 9 con 1 3 4 identificados como la primera mitad y los 3 se identifica como el centro de la primera mitad, 4 identificados como Q2, 5 7 9 identificados como la segunda mitad con 7 identificados como el centro de la segunda mitad.Puesto que cada mitad contiene un número impar de elementos, escoja el número medio por la mitad cada.
51 3 4 4 5 7 9 con 3 identificados como Q1, los segundos 4 identificados como Q2, y 7 identificados como Q3.El centro de la primera mitad y la segunda mitad son Q1 y Q3 respectivamente.
Cuadro 2: Ejemplo 1

PasoFiguraDescripción
1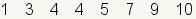1 3 4 4 5 7 9 10Éste es el grupo de datos a dividir en cuartilas.
21 3 4 4 5 7 9 10 con los segundos 4 y 5 identificados como el centro.Puesto que el grupo de datos tiene un número par de elementos, escoja los dos elementos medios para calcular el punto medio (Q2).
31 3 4 4 5 7 9 10 con los segundos 4 y 5 identificados como el centro. Se calcula Q2 como (4+5)/2=4.5.El punto medio (Q2) es el medio aritmético de los dos números medios.
41 3 4 4 5 7 9 10 con 1 3 4 4 identificados como la primera mitad, 4.5 identificados como Q2, y 5 7 9 10 identificados como la segunda mitad.El número medio divide el grupo de datos en dos mitades. Los dos números usados para calcular el punto medio se incluyen por la mitad.
51 3 4 4 5 7 9 10 con 1 3 4 4 identificados como la primera mitad y 3 4 se identifica como el centro de la primera mitad, 4.5 identificados como Q2, 5 7 9 10 identificados como la segunda mitad con (7+9)/2=8 identificado como Q3.Puesto que cada mitad contiene un número par de elementos, escoja los dos números medios por la mitad cada.
61 3 4 4 5 7 9 10 con 1 3 4 4 identificados como la primera mitad y (3+4)/2=3.5 se identifica como Q1, 4.5 identificados como Q2, 5 7 9 10 identificados como la segunda mitad con 8 identificados como Q3.Calcule Q1 como el medio aritmético de los dos números medios de la primera mitad. Calcule Q3 como el medio aritmético de los dos números medios de la segunda mitad.
71 3 4 4 5 7 9 10 con 1 3 4 4 identificados como la primera mitad y (3+4)/2=3.5 se identifica como Q1, 4.5 identificados como Q2, 5 7 9 10 identificados como la segunda mitad con 8 identificados como Q3.Para este grupo de datos Q1=3.5, Q2=4.5, y Q3=8.
Cuadro 3: Ejemplo 2

PasoFiguraDescripción
1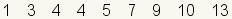1 3 4 4 5 7 9 10 13Éste es el grupo de datos a dividir en cuartilas.
21 3 4 4 5 7 9 10 13 con 5 identificados como el centro.Puesto que el grupo de datos tiene un número impar de elementos, escoja el elemento medio como el punto medio.
31 3 4 4 5 7 9 10 con 5 identificados como el Q2.Q2 es igual que el punto medio.
41 3 4 4 5 7 9 10 con 1 3 4 4 identificados como la primera mitad, 3 4 identificados como el centro de la primera mitad, 5 identificados como Q2, y 7 9 10 13 identificados como la segunda mitad, y 9 10 identificados como el centro de la segunda mitad.Q2 divide el grupo de datos en dos mitades. Puesto que las mitades tienen un número par de elementos cada uno, escoja los dos números medios de las mitades.
51 3 4 4 5 7 9 10 con 1 3 identificado mientras que el primer trimestre, 3.5 identificados como Q1, 4 4 identificó mientras que el segundo trimestre, 4.5 identificados como Q2, 5 7 identificó mientras que el tercer cuarto, 9.5 identificados como Q3, y 9 10 identificaron mientras que el tercer cuarto.Calcule Q1 y Q3 como el medio aritmético de los dos números medios.
Cuadro 4: Ejemplo 3

Citar este artículo como:
Cuartila. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/q/quartile.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-01-12: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License