ReflexiÃģn
|
Una reflexiÃģn es una transformaciÃģn geomÃĐtrica. En una reflexiÃģn, un objeto geomÃĐtrico âse mueve de un tirÃģnâ? a travÃĐs de una recta. La recta a travÃĐs de la cual se refleja un objeto se llama la recta de reflexiÃģn o el eje de la reflexiÃģn. El manipulante 1 demuestra la reflexiÃģn de un pentÃĄgono irregular a travÃĐs de una recta. Chasque encendido los puntos azules en el manipulante 1 y arrÃĄstrelos para cambiar la figura. Observe que la figura reflejada es una imagen de espejo de la figura original. Para ver la construcciÃģn de A y de B', chascar encendido las cajas de cheque. CaracterÃsticas de reflexiones
|
Construir una reflexiÃģn
| Paso | Figura | DescripciÃģn |
|---|---|---|
| 1 |  | Construiremos la reflexiÃģn del punto A a travÃĐs de la recta de reflexiÃģn. |
| 2 | 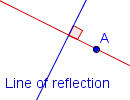 | Construya una recta perpendicular a la recta de reflexiÃģn que pase a travÃĐs del punto A. |
| 3 | 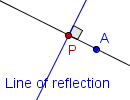 | Marque la intersecciÃģn de las rectas perpendiculares como P. |
| 4 | 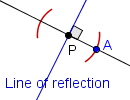 | Utilice un compÃĄs con el punto en P y la aguja en el punto A. Sin la eliminaciÃģn del punto de P, dibuje un arco circular en el lado opuesto de la recta perpendicular. |
| 5 | 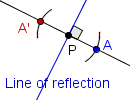 | Marque la intersecciÃģn del arco y la recta perpendicular como A'. |
| Cuadro 1: Construir la reflexiÃģn de un punto. | ||
| Paso | Figura | DescripciÃģn |
|---|---|---|
| 1 | 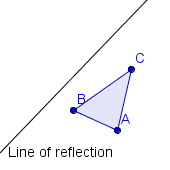 | ÂŋConstruiremos la reflexiÃģn de triÃĄngulo ΔABC a travÃĐs de la recta de reflexiÃģn. |
| 2 | 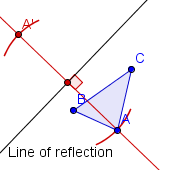 | Construya la reflexiÃģn de A a travÃĐs de la recta de reflexiÃģn (vÃĐase el cuadro 1). Etiquete el punto reflejado A'. |
| 3 | 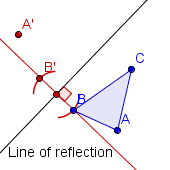 | Construya la reflexiÃģn de B a travÃĐs de la recta de reflexiÃģn. Etiquete el punto reflejado B'. |
| 4 | 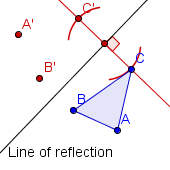 | Construya la reflexiÃģn de C a travÃĐs de la recta de reflexiÃģn. Etiquete el punto reflejado C'. |
| 5 | 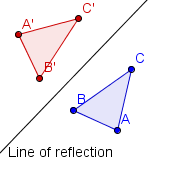 | Utilice un borde recto para conectar los puntos A', B y C con la recta segmentos. El triÃĄngulo ΔA'B'C' estÃĄ la reflexiÃģn de triÃĄngulo ΔABC a travÃĐs de la recta de reflexiÃģn. |
| Cuadro 1: Construir la reflexiÃģn de un triÃĄngulo. | ||
MÃĄs informaciÃģn
- reflexiÃģn. buscon.rae.es. Real Academia EspaÃąola. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=reflexiÃģn.
Citar este artÃculo como:
ReflexiÃģn. 2009-04-03. Enciclopedia de Todas las Palabras de la MatemÃĄticas. Life is a Story Problem.org. https://www.allmathwords.org/es/r/reflection.html.
Traducciones
crÃĐditos de imagen
- Todas las imÃĄgenes y manipulatives estÃĄn por David McAdams a menos que estÃĐn indicadas de otra manera. Todas las imÃĄgenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisiÃģn
2009-04-03: Traducido automÃĄticamente por BabelFish. (babelfish.yahoo.com.)
2009-01-13: VersiÃģn inicial (McAdams, David.)
- NavegaciÃģn
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la MatemÃĄticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ÂĐ2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License